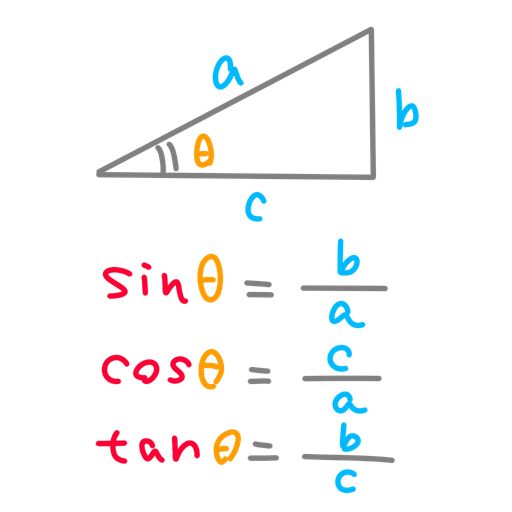【Houdini HDA 講座】#3 VEX・エクスプレッションの基礎
✦ 今回の目標
今回は今まで進めてきた家の制作からいったん離れ、 VEX とエクスプレッションを理解します。
※なので、 #1 と #2 を見ていなくても理解できるようになっています。
プログラミングを全く触ったことが無い人には少し難しいかもしれませんが、できるだけ丁寧に解説します。
✦ VEXとエクスプレッションの違い
以前にも少し出てきましたが、Houdini にはプログラミング言語が VEX とエクスプレッションとで2つ存在します。
両者はよく似ていますが別の言語です。
VEX は基本的に wrangle SOP 内に記述する言語で、C言語などに近い言語です。
複数行のプログラムを組むような前提の言語です。
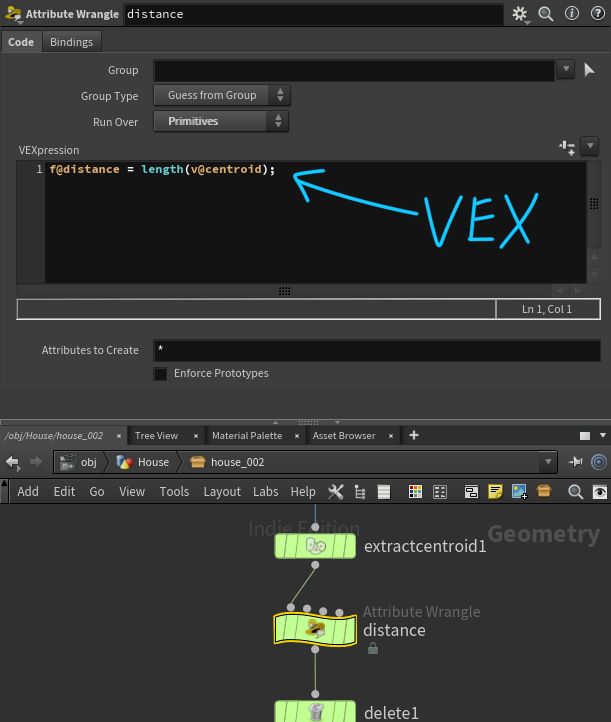
前回の初めの方に追加した attribute wrangle SOP(distance と改名したもの)に書いてあるプログラムが VEX です。
それに対してエクスプレッションはパラメータの入力欄に記述し、1行で記述を終わらせることが多い簡易的な言語です。
エクセルで言うと、 VEX が Visual Basic で エクスプレッションがセルに記述する関数のような立ち位置です。
エクスプレッションをパラメータ欄に記述すると、パラメータ欄が緑色になります。
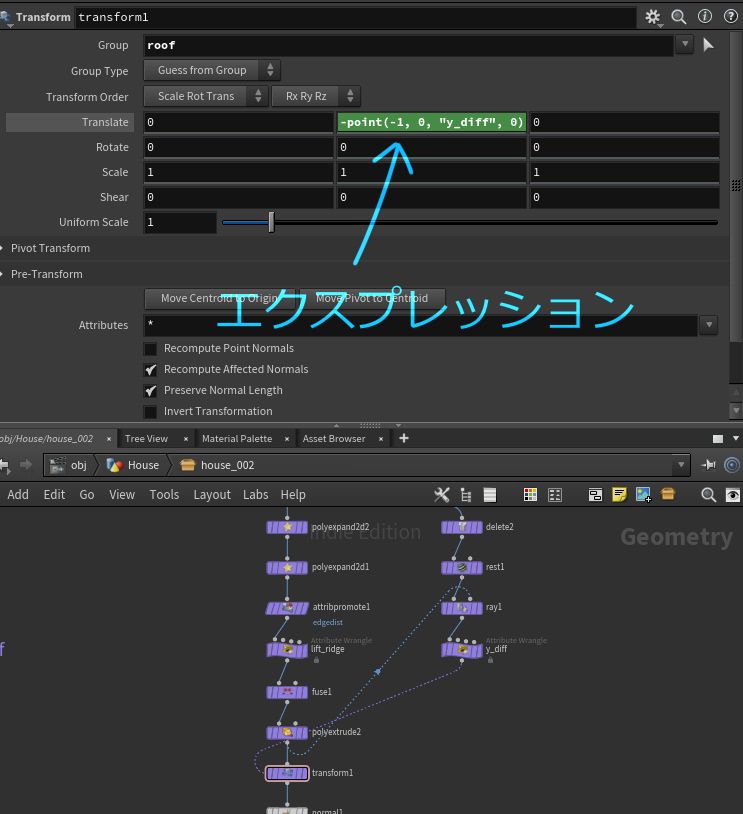
前回の最後の方に追加した transform SOP で記述した -point(-1, 0, "y_diff", 0) はエクスプレッションです。
VEX とエクスプレッションは別言語ですが寄せて作られているので、同じように関数を使うことができることもあります。
ただし、基本的には別言語だということを押さえておきましょう。
✦ VEX の基礎
VEX 言語で特に使用頻度の高い機能を紹介します。
基本的にはC言語と似ていますが、3Dプログラミング向けにカスタマイズされています。
一度家の制作から離れ、VEX のテスト実行を行うための環境を作りましょう。
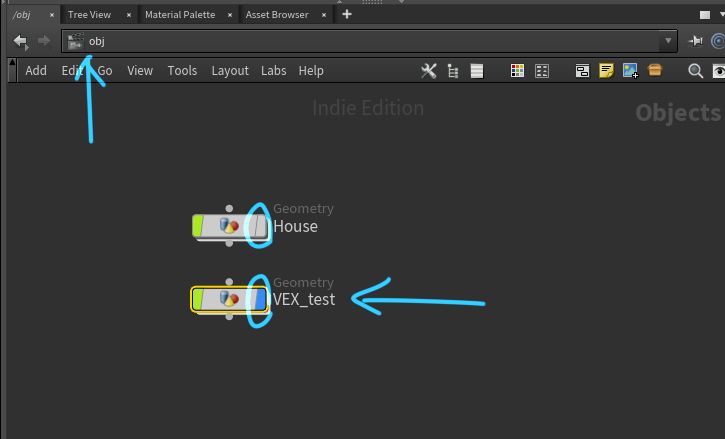
Network View で obj 階層に戻り、Geometry ノードを作成し、名前を「VEX_test」とします。
House が表示されないようにするため、 Display フラグを VEX_test だけに立てます。
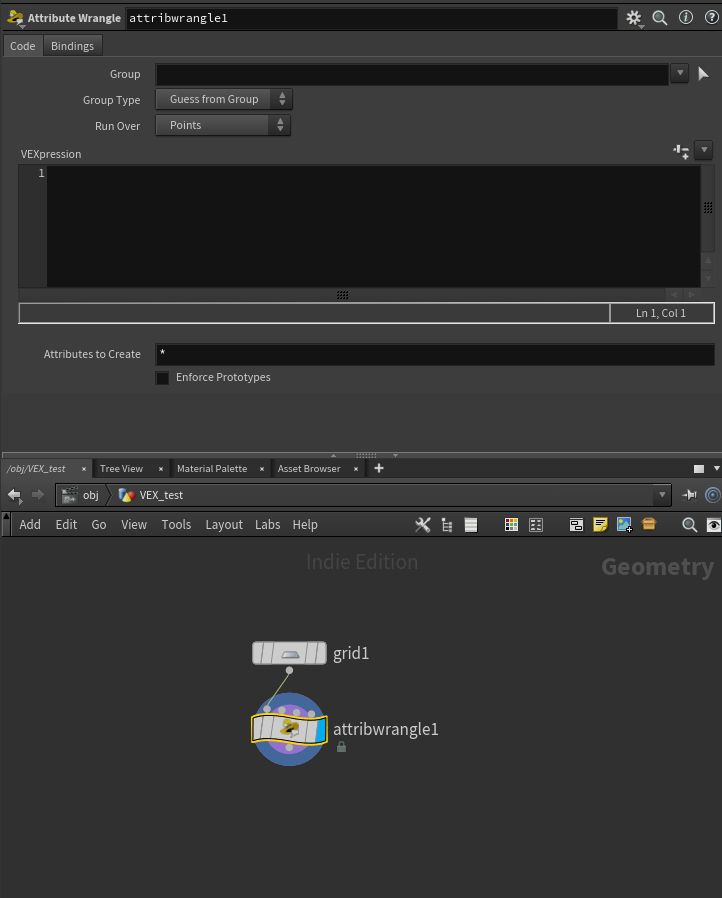
VEX test をダブルクリックし、中に入ります。
そして、 grid SOP と attribute wrangle SOP を配置し、つなぎます。
この attribute wrangle SOP にこれから出てくるサンプルコードを書きこんで試してみてください。
✦ 変数
変数には値(数字や文字列など)を保存できます。
C言語と同じで型があります。
- int:整数
- float:小数
- vector:ベクトル
- string:文字列
型 変数名;という形で変数を作ります。
変数名 = 値;という形で値を変数の中に入れます。(代入)
行末には ; が必須です。
int a;
a = 10;
このように書くと、 a の中に 10 が入ります。
他の型の書き方は以下のような感じです。
float b;
b = 10;
vector c;
c = {1, 0, 0};
ベクトルは 3 次元ベクトルです。
二次元ベクトル(vector2)や四次元ベクトル(vector4)、マトリクス(Matrix)なども存在します。
string d;
d = "Houdini";
string は文字列です。
文字列の値を表す際には "文字列" とダブルクォーテーションで囲みます。
変数を宣言すると同時に代入する初期化もできます。
int a = 11;
float b = 2.3;
vector up = {0, 1, 0};
string str = "Houdini";
一般的な言語と同じです。
✦ 関数
他の言語と同じですが、値を処理するのが関数です。
関数名(引数) という形で使います。
引数は関数に渡す値のことです。
引数が複数必要な関数は 関数名(引数, 引数, 引数) といった形でカンマ区切りになります。
引数の数やどういった値を入れるのかは関数ごとに決まっています。
Houdini には VEX で使える関数がたくさん用意されています。
例として、 printf 関数を使ってみましょう。
以下のコードを先ほど用意した attribute wrangle ノードの VEXPression に記述してみましょう。
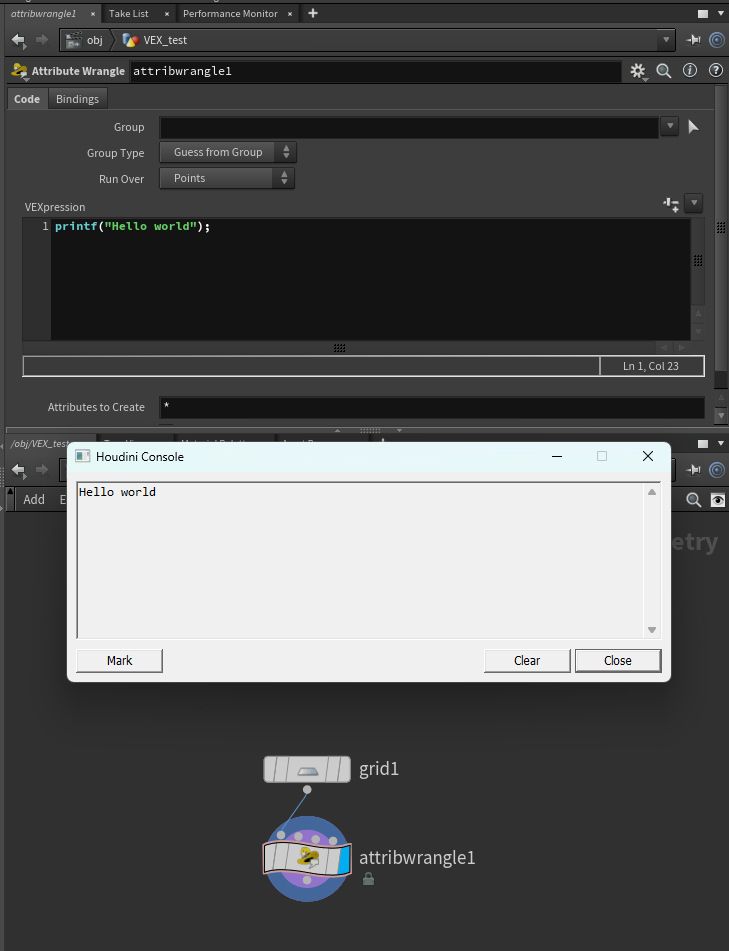
printf("Hello world");
すると、以下のようにコンソールのウィンドウが出てきて、 Hello world と表示されます。
printf 関数はこのようにコンソールに値を表示するための関数です。
変数の中の値を表示するためには、以下のようなフォーマット(書き方)を使用します。(printf の f はフォーマットの f です)
int a = 100;
printf("%d", a);
このコードを attribute wrangle SOP に記述すると、コンソールに 100 と表示されます。
フォーマットの詳しい解説は今回は避けますが、%g (おそらく general の g です)が色々表示出来て便利です。
気になる方は以下のページを参照してください。
他にもよく使う関数を軽く紹介します。
✦ 数学的な関数
学校の授業で出てくるような関数も大体用意されています。
使い方の前に、まずはどんな関数が用意されているか紹介します。
✦ 三角関数
三角関数は学校の授業で習ったままの関数名になっています。
- sin 関数
- cos 関数
- tan 関数
後で家を作るときに時に使うので sin, cos, tan を復習しておきましょう。
直角三角形のそれぞれの2辺の比率を斜辺の角度で表す関数です。
✦ べき乗、平方根(ルート)
- pow 関数(べき乗)
- sqrt 関数(平方根)
学校では右上に数字を小さく書いて表記したり、 √ を書いて表したりしていましたが、アルファベット名の関数になっています。
それぞれ、 power と square root の略です。
このような関数名も他の言語でも一般的です。
✦ 切捨、切上、四捨五入
この辺りもほかのプログラムミング言語でも一般的な名前がついています。
- ceil 関数(切り上げ)
- floor 関数(切り捨て)
- rint 関数(四捨五入)
ceil は天井、 floor は床、rint は round to integer の略です。
✦ 返り値を返す関数の使い方
使い方は基本的には printf 関数などと同じで 関数名(引数) の書き方ですが、これらの関数は printf 関数とは違い処理結果の数値が存在します。
その処理結果をどうやって扱うかという話になります。
結論、このような形で扱います。
float a = 4.2;
float b;
b = rint(a);
上記のように記述すると、 b の中に 4 が入ります。
以下のように書いても同じです。
float a = 4.2;
float b = rint(a);
float b = rint(4.2);
数学系の関数に限らず、関数の引数には変数に入れた値を使うこともできますし、直に値を使うこともできます。
このように、処理結果が存在する関数を"返り値を返す関数"と呼び、処理結果のことを"返り値"と呼びます。
先ほどの例で言うと 4.2 が返り値で、 rint は返り値を返す関数です。
(printf 関数は画面にコンソールを出すという処理をしますが、処理結果の値は返しません。処理結果を返さない場合 void を返すと表現することもあります。void とは空ということです。)
返り値のイメージは、先ほどの例で言うと rint(4.2) と記述するとその部分が 4 という値に変換されてその部分は 4 として処理されるというイメージです。
b = rint(4.2) の関数部分が処理されると b = 4 になるという感じです。
✦ ベクトル操作
3D データを扱うソフトとしてベクトルの操作を行う関数も揃っています。
よく使う関数を紹介します。
- normalize 関数(正規化)
- length 関数(長さ)
- dot 関数(内積)
- cross 関数(外積)
normalize 関数はベクトルの向きを変えずに長さが1になるようにベクトルを変換します。
vector a = {3, 0, 0};
vector b = normalize(a);
とすると、 b の値は {1, 0, 0} になります。
この関数は非常によく使うので覚えておいてください。
length 関数はベクトルの長さを返します。
vector a = {3, 0, 0};
float b = length(a);
とすると、b の値は 3 になります。
dot (内積)や cross (外積)もよく使用するので、次の回(#4)で具体的に使用しながら説明します。
✦ アトリビュートの読み取り
Geometry Spreadsheet で確認できるアトリビュートを VEX 内で利用するためには以下の関数を使います。
よく使う関数は以下です。
- point 関数
- vertex 関数
- primitive 関数
- detail 関数
point, vertex, primitive, detail とジオメトリスプレッドシートのどこから値を持ってくるかで関数が分かれています。
point(ジオメトリ, アトリビュート名, ポイント番号) といった形で書きます。
どの表の、どの列の、どの行というのを指定するイメージです。
それぞれの引数について説明します。
ジオメトリは、どのジオメトリ(3Dモデル)からアトリビュートを取得するかの指定です。
数字で入力することができます。
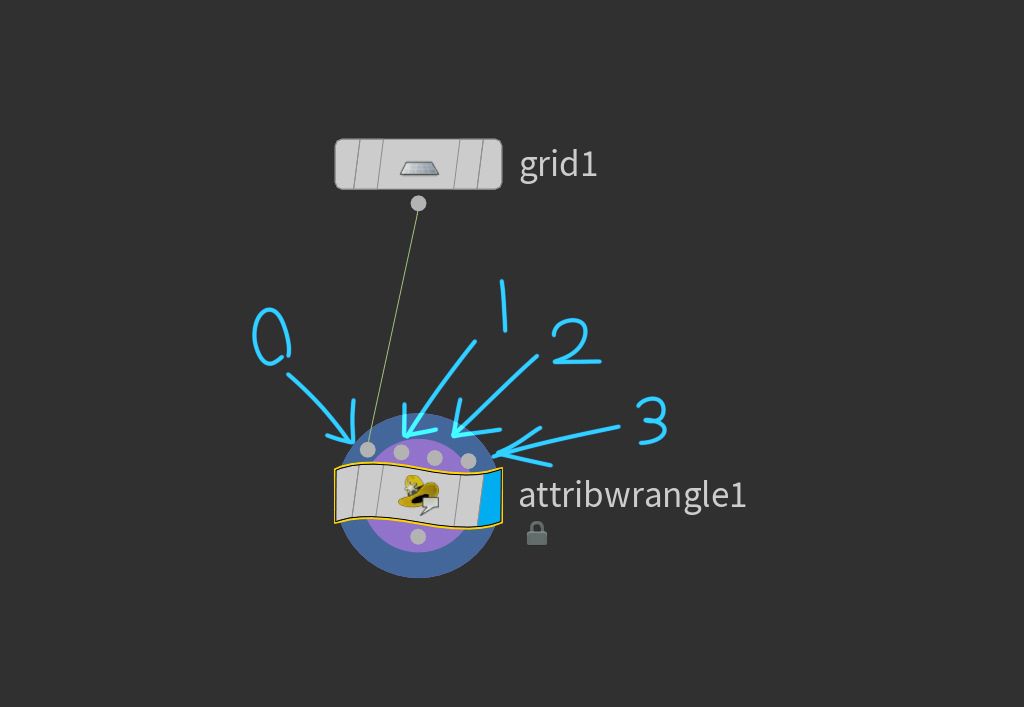
例えば、各ノードの入力には左から 0, 1, 2 ... と番号が振り分けられています。
画像のように grid1 ノードと input 0 でつながっている場合は 0 と指定することで grid1 のジオメトリを指定できます。
前回出てきた Spare Input (紫の点線のつながりです)は -1, -2 -3 ... と負の番号が割り当てられています。
1つ目の Spare Input が -1 で、2つ目の Spare Input が -2 とうことです。
※ジオメトリの指定に "./grid1" といった形で文字列でパスを指定することもできますが、個人的にはあまりオススメしません。(ノードが視覚的に線でつながらないので、どこから値を持ってきたか分かりずらくなってしまうからです。)
※この辺りの定義はかなり Houdini 独特です。
アトリビュート名は、P, N, Cd, や前回出て来た edgedist のようなアトリビュートの名前です。
ダブルクォーテーションで囲い、文字列で指定します。
ジオメトリスプレッドシートの列にあたります。
ポイント番号は何番目のポイントかを指定する数字です。
ジオメトリスプレッドシートの行にあたります。
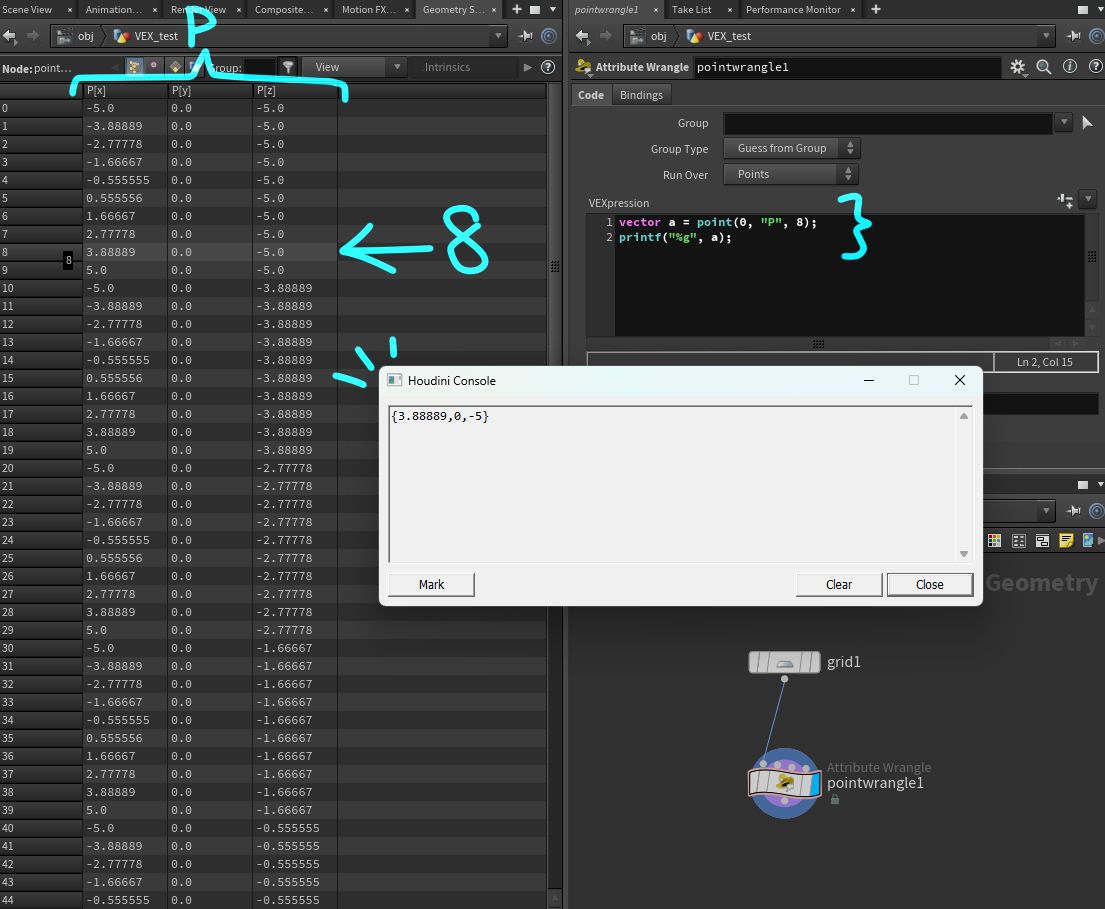
例として、 VEX_test の wrangle SOP に以下のコードを書いてみましょう。
vector a = point(0, "P", 8);
printf("%g", a);
すると、コンソールウィンドウに {3.88889,0,-5} と表示されます。
入力 0 の 8 行目の P の値を取得して表示しています。
✦ アトリビュートの書き込み
アトリビュートの読み取りに対して、書き込みの関数も存在します。
- setpointattrib 関数
- setvertexattrib 関数
- setprimattrib 関数
- setdetailattrib 関数
setpointattrib(ジオメトリ, アトリビュート名, ポイント番号, 値) という使い方で、最後に書きこむ値を指定する引数ありますが、それ以外の引数は読み込みの関数と同じです。
例として、以下のコードを wrangle SOP に記述してみましょう。
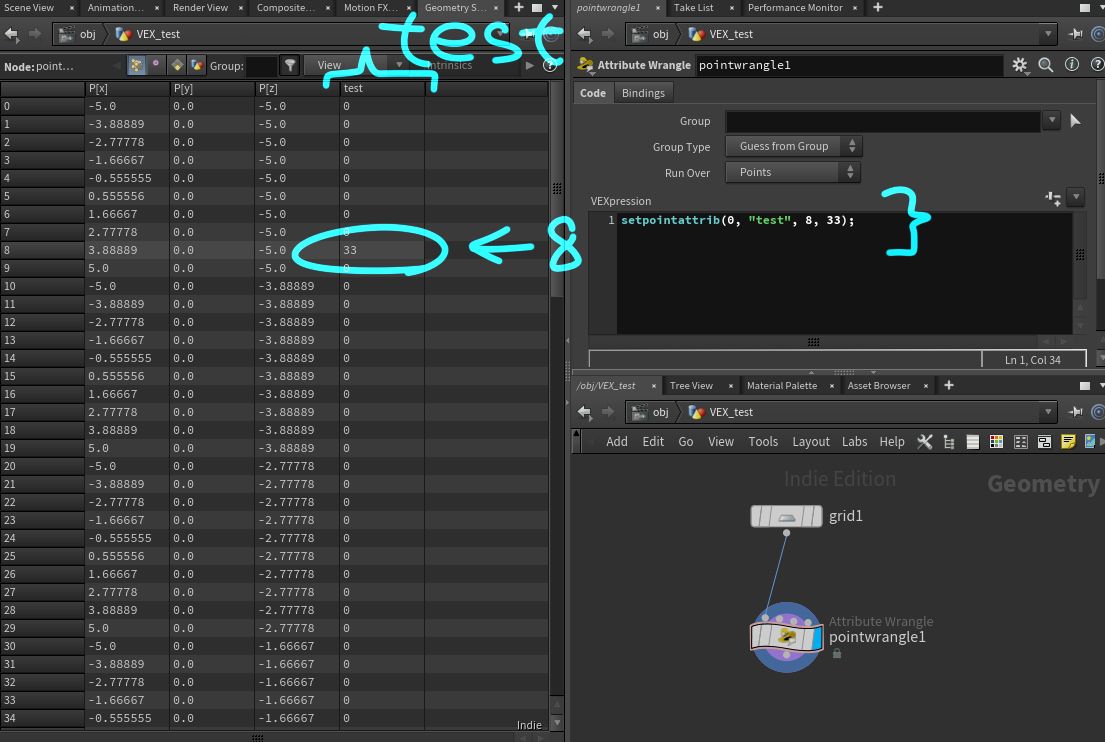
setpointattrib(0, "test", 8, 33);
画像のように、 test アトリビュートが増えて 8 番目に 33 が入ります。
指定したアトリビュート名のアトリビュートが存在すればそのアトリビュートに書きこみを行いますが、無い場合は新しくアトリビュートを作成します。
次に以下のように記述してみましょう。
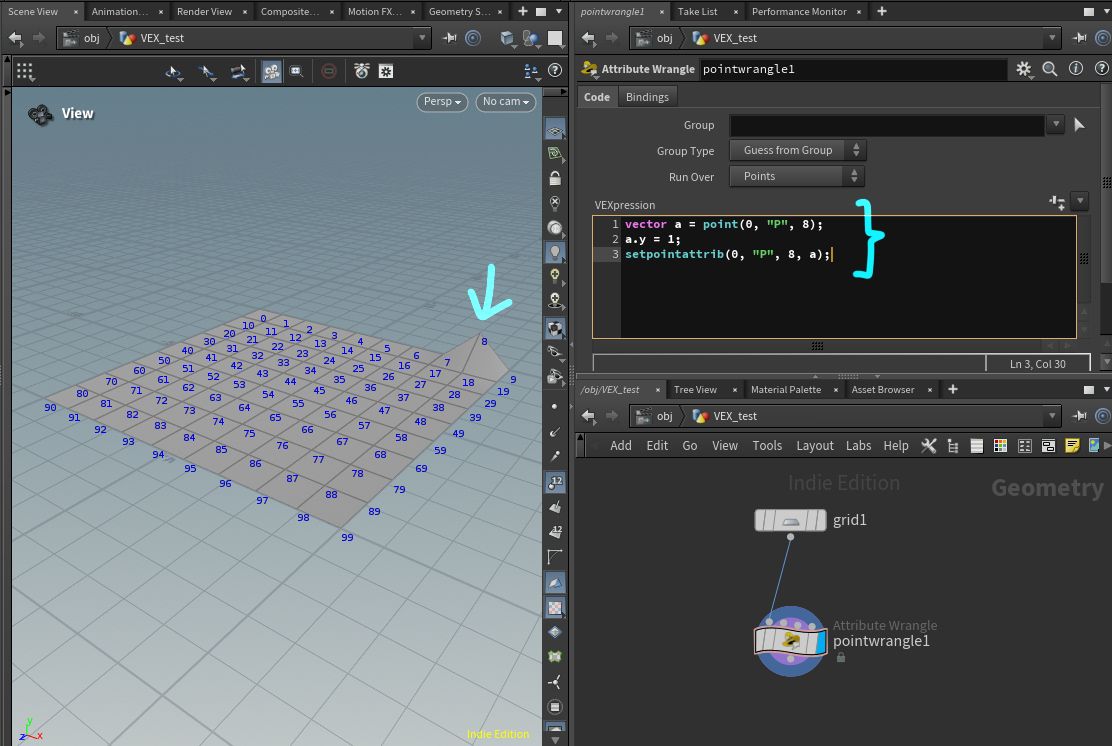
vector a = point(0, "P", 8);
a.y = 1;
setpointattrib(0, "P", 8, a);
すると、画像のように 8 番目のポイントが上に移動します。
a.y というのはベクトルの変数 a の y 要素(上下方向)です。
8 番目の要素を取得して、 y を 1 にしてから再度元の 8 番目の要素に書きこんでいます。
✦ @ 記法
Houdini 独特の記法で、 @ というものがあります。(名前が分かりませんw)
この記法でアトリビュートの読み取りと書きこみを簡易的に行うことができます。
ただし、先ほどの point 関数や setpointattrib 関数よりも限定的な用途になります。
point 関数や setpointattrib 関数では、ジオメトリやポイント番号(行)を自由に指定できましたが、 @ を使う場合はアトリビュート名しか指定できません。
どういうことか、例を見てみましょう。
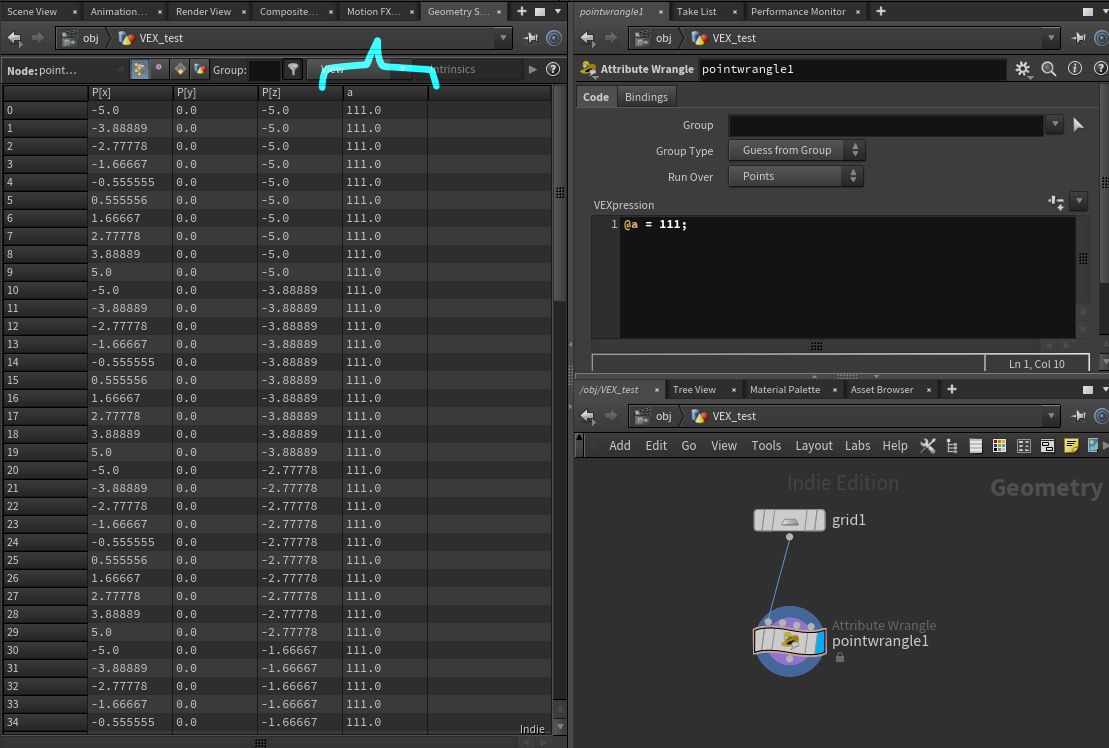
@a = 111;
上記のように @アトリビュート名 という形で使います。( attribute → at → @ なのかなと勝手に思ってます)
これを、 wrangle SOP に記述すると、以下の画像のような結果になります。
全ての行の a アトリビュートに 111.0 が入りました。
ここまであえて曖昧にして進めていたのですが、 point wrangle SOP では VEX が全ての行で実行されます。
grid1 SOP では 100 個のポイントが生成されるため、VEX は 100 回実行されます。
( setpointattrib も実は 100 回実行されていました。 printf 関数が 100 回 "Hello world" を表示しなかったのは、同じものを大量に出力しても仕方がないので気を利かせるようになっているのだと思います。)
したがって、 @a=111; として代入するとすべての行の a アトリビュートに 111 が入るというわけです。
@a = 111; は以下のように書いても同じ意味になります。
setpointattrib(0, "a", @ptnum, 111);
ここで、 @ptnum という新しい @ 記法の記述が出てきました。
同じ記法ですが、ptnum は特殊なアトリビュートです。
@ptnum はポイント番号(point number)を表します。
つまり、ジオメトリスプレッドシートの一番左の列の数字です。
それぞれの行で VEX が実行される際に、処理している行がどの行かを表す数字を取得できます。
今回の場合、VEX が100回実行される際に 0 行目での実行の際には @ptnum には 0 が入っていて、 1 行目での実行実行では 1 が入っていて…ということです。
したがって先ほどの @a = 111; はジオメトリが 0 で固定で、それぞれの行の処理でその行に 111 を入れるということになるので、 setpointattrib(0, "a", @ptnum, 111) と同じ意味になります。
また、 Run Over が primitive に設定されている wrangle SOP では @primnum と記述することで primitive の番号を取得できます。
同様に以下が存在します。
- @ptnum
- @vtxnum
- @primnum
これらは読み取り専用で、書き込みはできません。(この点が通常の @ と比べて特殊です)
先ほど @a = 111; として書き込みを行いましたが、読み取りもできます。
以下のように記述してみましょう。
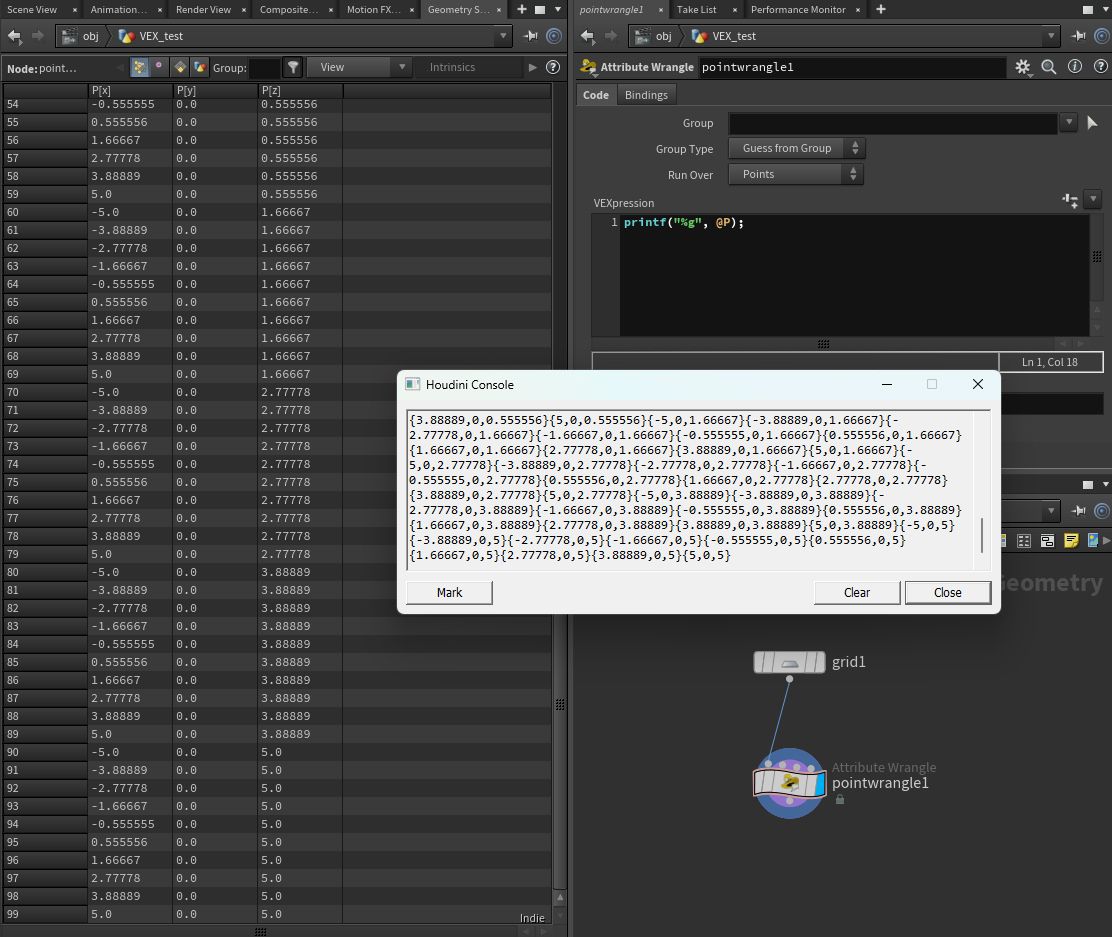
printf("%g", v@P);
画像のように、それぞれの行の P (座標)が出力されます。
@ の前の v は vector の v です。
つまり、アトリビュートをどの型で取り出したいかを指定しています。
(float 型のアトリビュートを int 型で取り出したりといったことも一応できます。)
型を指定しないと意図とは違う型で取り出される場合があるのでできるだけ @ の前に型を書くことをおすすめします。
代表的な型のそれぞれの記号は以下の通りです。
i(int:整数値)f(float:小数値)v(vector:ベクトル)s(string:文字列)
✦ 演算
足し算、引き算、掛け算、割り算といった演算は関数を使わずにそのまま書くことができます。
各演算子(演算に使う記号)は以下の通りです。
+(足し算)-(引き算)*(掛け算)/(割り算)++(インクリメント:+1 と同じ)--(デクリメント:-1 と同じ)%(剰余:割り切れずに余った数)
この演算は変数や値に対して基本的にどこでも使うことができます。
int a = 10 + 2;
この場合、 a は 12 になります。
また、 以下のようなものもあります。
+=-=*=/=%=
例えば、 a += b; は a = a + b; と同じです。
これらの右側に = のついている演算子は代入を行いながら演算をするというイメージです。
float b = 5 / 2;
b は 2.5 になります。
printf("%g\n", 100 % 30);
コンソールには 10 と表示されます。
int a = 1;
++a;
a は 2 になります。
また、関数や演算子などの処理される順番には優先順位が決まっています。
int a = 2 + 3 * 4;
この場合は 3 * 4 が優先されて a は 14 になります。
int a = ( 2 + 3 ) * 4;
しかしこの場合は、 ( 2 + 3 ) にカッコがついているのでこちらが優先されて a は 20 になります。
✦ if 文
ある条件を満たす場合にのみ処理を実行する場合には、 if 文を使います。
形式としては以下のような感じです。
if(条件式){
処理
}
{ と } で囲われた処理が、 if( と ) で囲われた条件式を満たす場合にのみ実行されます。
この書き方はプログラミング言語を問わず一般的です。
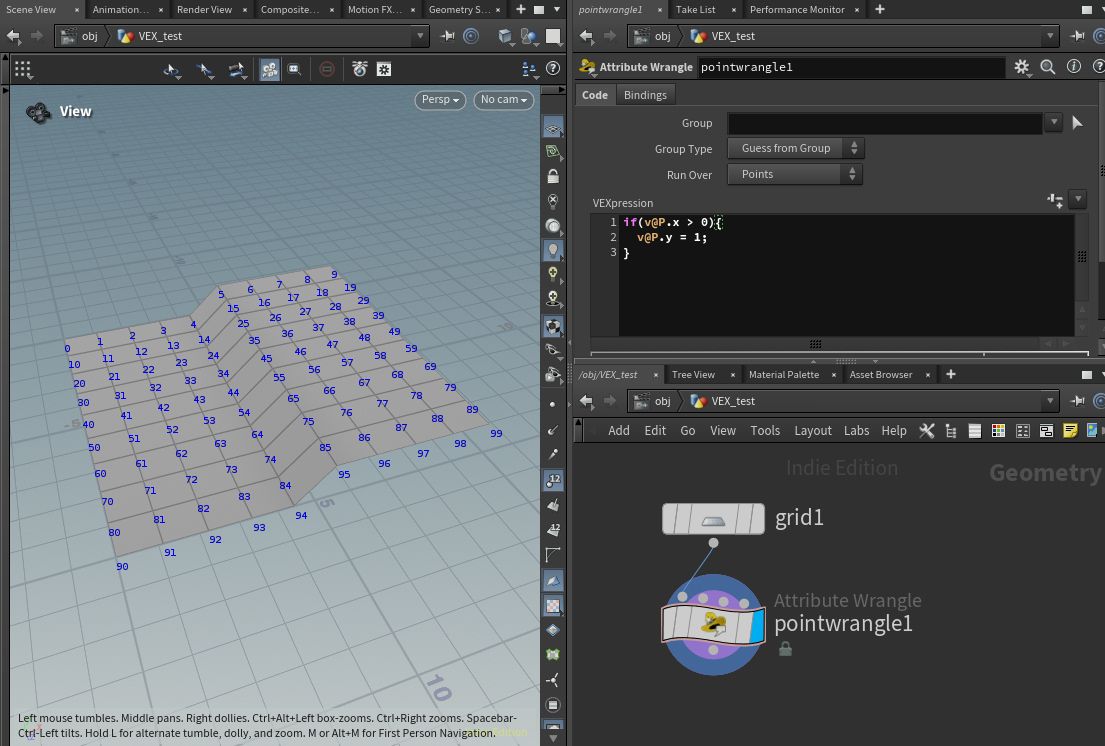
例えば、以下のように記述してみましょう。
if(v@P.x > 0){
v@P.y = 1;
}
すると、以下のような結果になります。
x 座標が 0 以上のポイントが上に上がりました。
v@P.x > 0 が条件式で、条件式とは真と偽に結果が二分される演算の式のことです。
v@P.x > 0 は P アトリビュートの x 座標が 0 より大きいかどうかを判定します。
真の場合( 0 より大きい場合)は条件式は 1 となり、偽の場合( 0 以下の場合)は条件式は 0 となります。
※Houdini では真偽は int 型の 0, 1 で表します。(珍しいです。)
以下のように記述すると、 a には 1 が入ります。
int a = (2 > 1);
> を比較演算子といい、他にも以下のようなものがあります。
>(大なり)<(小なり)>=(大なりイコール)<=(小なりイコール)==(イコール)
※ ( ) で囲んでいるのは単純に見ずらいからです。
今まで変数に値を入れるのに使っていたのは = ですが、比較演算のイコールは == なので注意です。
ちなみに、関数の中にも 0 か 1 (真偽値)を返す関数があります。
if 文に対応して、条件が満たされなかった場合に別の処理を実行するためには else 文を使用します。形式は以下の通りです。
if (条件式) {
// 条件式が 1 の場合の処理
} else {
// 条件式が 0 の場合の処理
}
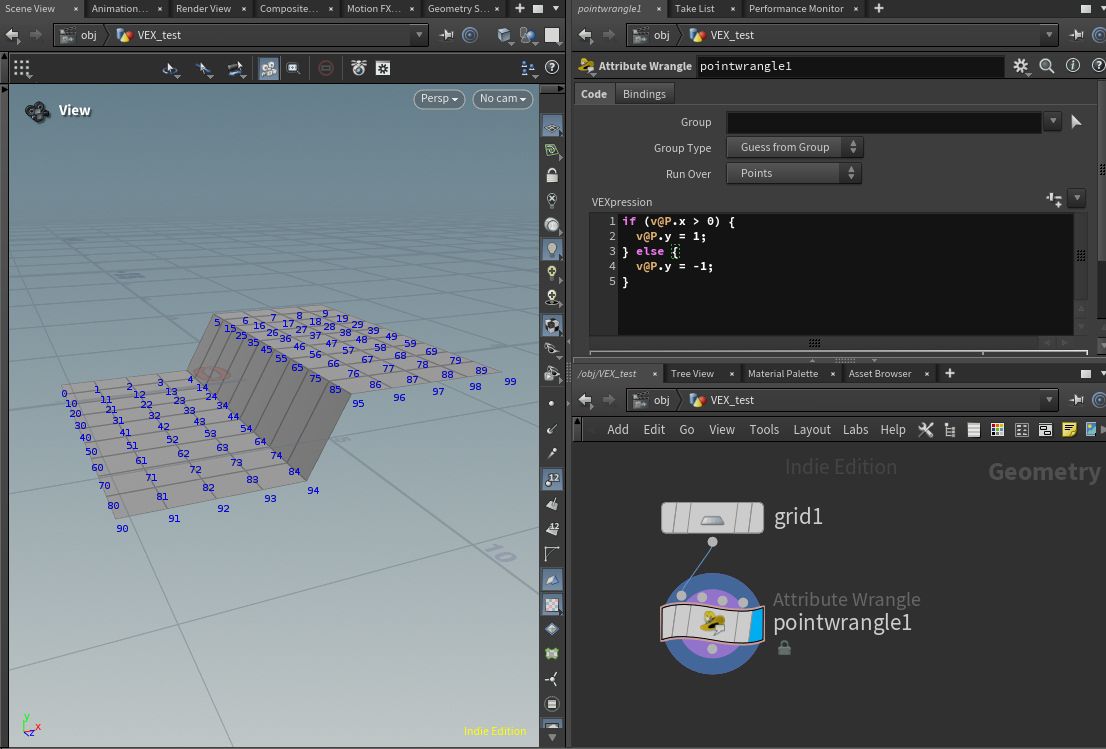
例えば、以下のように記述してみましょう。
if (v@P.x > 0) {
v@P.y = 1;
} else {
v@P.y = -1;
}
これを記述すると以下のようになります。
複数の条件をチェックする場合には else if 文を使用します。形式は以下の通りです。
if (条件式1) {
// 条件式1が真の場合の処理
} else if (条件式2) {
// 条件式2が真の場合の処理
} else {
// 条件式1, 条件式2がどちらも偽の場合の処理
}
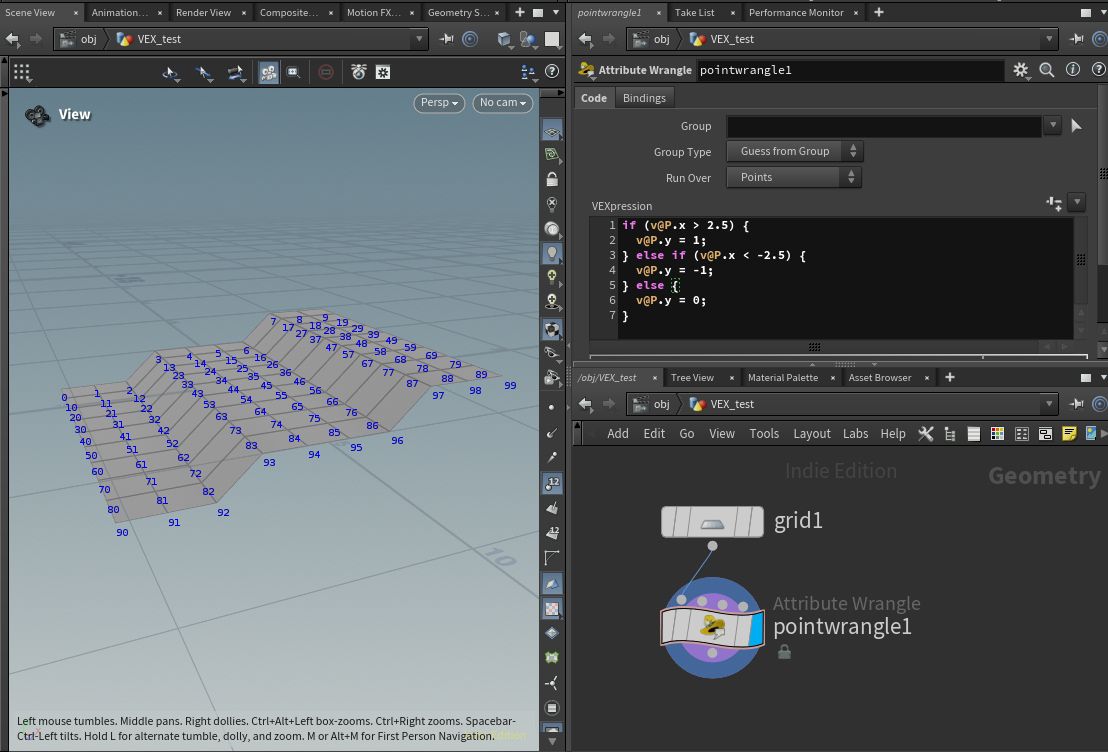
例えば、以下のように記述してみましょう。
if (v@P.x > 2.5) {
v@P.y = 1;
} else if (v@P.x < -2.5) {
v@P.y = -1;
} else {
v@P.y = 0;
}
これを記述すると以下のようになります。
✦ for 文
繰り返し処理を行う場合には for 文を使用します。形式は以下の通りです。
for (初期化; 条件式; 更新) {
// 繰り返し処理
}
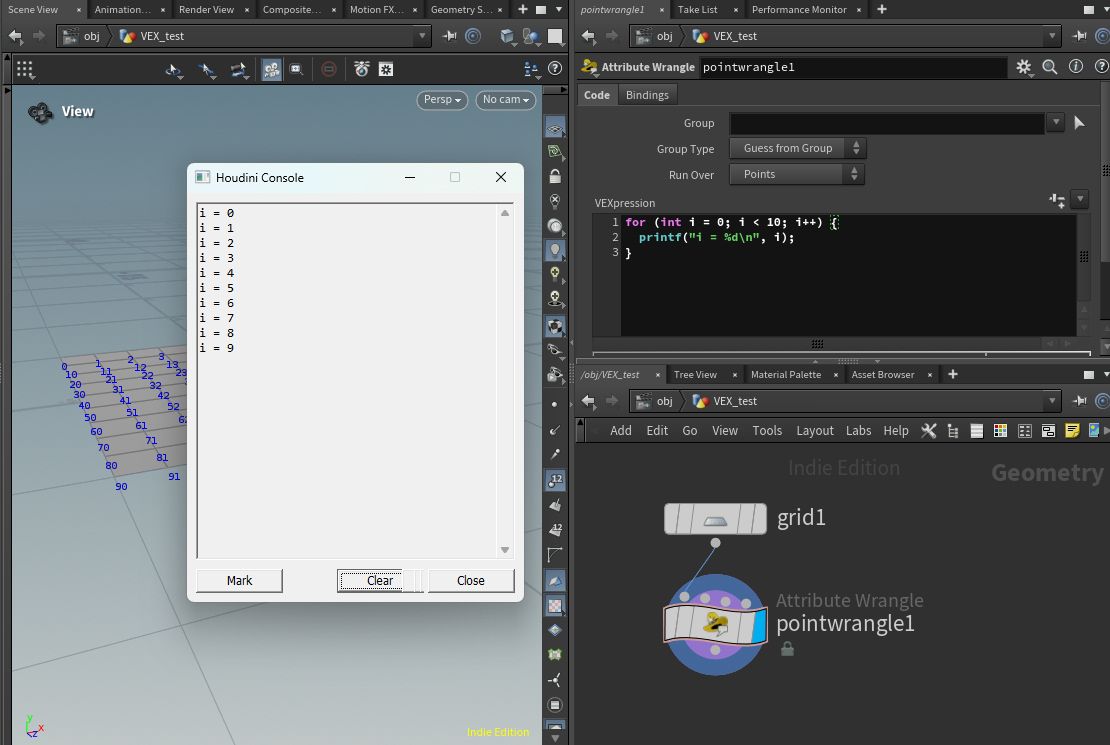
例えば、以下のように記述してみましょう。
for (int i = 0; i < 10; i++) {
printf("i = %d\n", i);
}
これにより、0 から 9 までの数値が出力されます。
for 文の各部分の意味は次の通りです。
基本的な使い方は、
-
初期化部分で変数を作って初期化(値の代入)をします。
-
条件式部分でが 1 (真)であれば、繰り返しが続行されます。
-
更新部分で変数を更新します。
基本的には先ほどのコードのように ( ) 内は int i = 0; i < 10; i++ の 10 の部分を変更して反復回数を変えることが多いです。
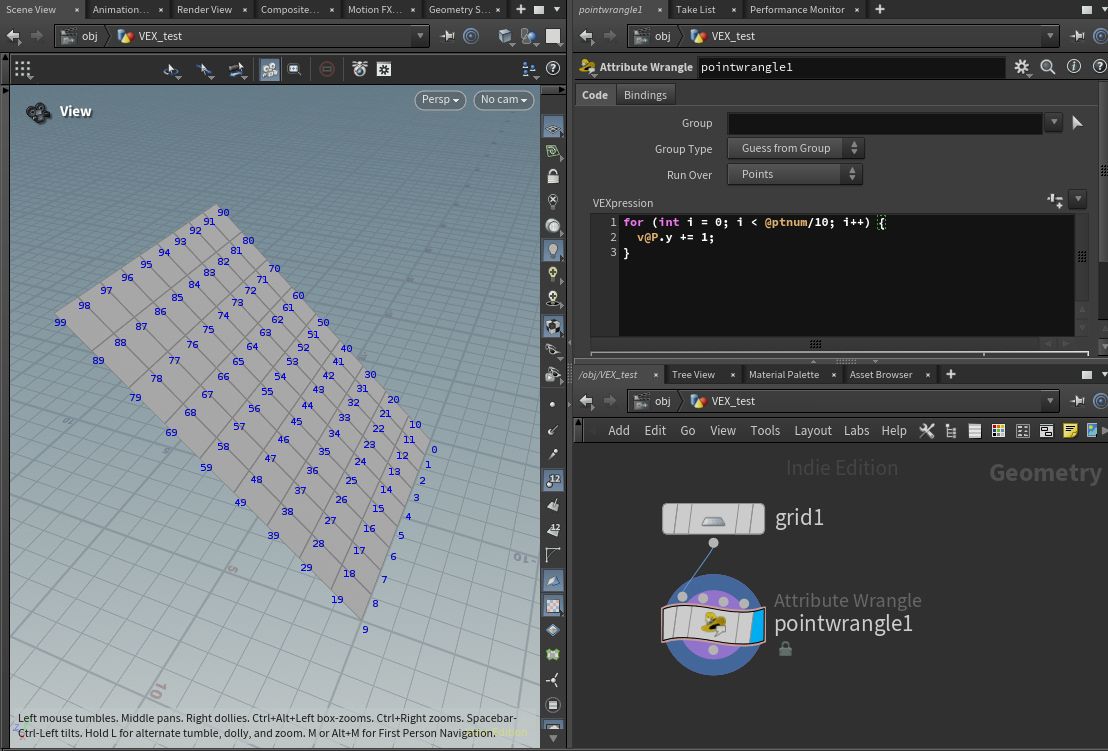
for (int i = 0; i < @ptnum/10; i++) {
v@P.y += 1;
}
このように記述すると以下のような結果になります。
それぞれの点で、その点のポイント番号 @ptnum を 10 で割った階数だけ y 座標が加算されています。
✦ その他
その他、代表的な機能では、配列 や foreach などが存在しますが今回の講座では割愛します。
✦ エクスプレッション
エクスプレッションには、 VEX と似たような関数がたくさん用意されています。
しかし冒頭でも説明した通り、別の言語なので関数の引数や返り値などの仕様が異なります。
例えば、 point 関数(ポイントのアトリビュート読み取り)は point(ジオメトリ, ポイント番号, アトリビュート名, アトリビュート番号) となっていて、VEX の point 関数と比べてアトリビュート番号が必要になっています。
アトリビュート番号にはアトリビュート内で何番目のものを取り出すかを指定します。
P であれば x, y, z がそれぞれ 0, 1, 2 に対応しています。
x, y, z のように複数の要素が無い場合は 0 を記述しておきます。
(同じ機能でも関数の名前が VEX と異なる場合もあります。)
また、演算子は VEX と同じように使用できます。
ただし、 if や for などは使えません。(一応、if 関数は用意されています。)
エクスプレッションでは基本的に、一行で事足りるちょっとした計算をすることが多いです。
複数行になる処理や複雑な処理をエクスプレッションでするのは避けて、処理は wrangle を用いて vex で行い、その結果をエクスプレッションで受け取るようにするのがおすすめです。